Vergelijkingen » Bordjesmethode
Inhoud
1. Wat is de bordjesmethode?2. Hoe werkt de bordjesmethode?
3. Kwadratische vergelijkingen
4. Hoe weet ik nu waar ik het bordje moet leggen?
Let op:
Heb je een vergelijking met aan beide kanten van het =-teken een variabele, dan kan je de bordjesmethode niet gebruiken.
Heb je zoiets als 3x + 5 = 7x – 2, kijk bij balansmethode.
Heb je zoiets als 5x2 + 3x = 2x + 4, kijk bij kwadratische vergelijkingen.
1. Wat is de bordjesmethode?
De bordjesmethode is een simpele manier om vergelijkingen op te lossen. Het heeft veel weg van stipsommen of vleksommen zoals je die op de basisschool hebt gehad.
Op iets wat je niet weet leg je een 'bordje'. Je gaat dan teruguit rekenen wat er voor een getal bij dit bordje hoort.
Je schrijft het bordje over met het getal dat het moet wezen.
Uiteindelijk weet je de onbekende waarde van de variabele.
2. Hoe werkt de bordjesmethode?
Volg het stappenplan hieronder:
1. Neem de vergelijking over in je schrift.
2. Schrijf indien mogelijk de vergelijking korter.
3. Teken een bordje op de juiste plaats* en schrijf dit eronder over.
4. Reken uit welk getal er op het bordje moet staan.
5. Bereken de oplossing.
(6. Controleer je oplossing door je antwoord in te vullen in de formule)
* De juiste plaats is op de variabele en wat er volgens de voorrangsregels bij hoort. Zie kopje 4 onder aan de pagina voor meer uitleg.
Voorbeeld 1
Controle: 25 + 5 × 12 = 85 |
Voorbeeld 2
Controle: 170 – 14 × 7 = 72 | ||||||||||||||||
Voorbeeld 3
Controle: 3 × –712 – 12 = –3412 |
Voorbeeld 4
Controle: 5(4 × –312 – 8) + 3 = –107 | ||||||||||||||||
3. Kwadratische vergelijkingen
De variabele in de vergelijking mag maar aan één kant van het =-teken voorkomen. Is dit niet het geval, kijk dan bij kwadratische vergelijkingen.
Je blijft net zo lang bordjes leggen tot je alleen de variabele overhoudt.
Let op: Er zijn vaak twee oplossingen!
Het moment dat je het kwadraat wegwerkt, krijg je deze twee oplossingen.
Voorbeeld 1
Controle: 4 + 3 × 72 = 151 |
Voorbeeld 2
Controle: –2 × ( 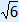 )2 – 5 = –17 )2 – 5 = –17
| ||||||||||||||||
Voorbeeld 3
|
Voorbeeld 4
Controle: (3 × 4 + 1)2 = 169 (3 × –423 + 1)2 = 169 | ||||||||||||||||
Voorbeeld 5
Controle: (2 × 5 – 2)2 + 4= 68 (2 × –3 – 2)2 + 4 = 68 | |||||||||||||||||
4. Hoe weet ik nu waar ik het bordje moet leggen?
Als het goed is ken je de rekenregels (voorrangsregels) voor het rekenen.
Zorg altijd dat je het bordje legt op alles behalve wat je volgens de formule als laatste zou moeten uitvoeren.
Als we kijken naar voorbeeld 1 van kopje 2, dan is de formule 40 + 5a.
Omdat we eerst moeten vermenigvuldigen en daarna pas moeten optellen wordt optellen als laatste gedaan en komt het bordje op alles behalve het getal wat opgeteld moet worden.
Als we kijken naar voorbeeld 1 van kopje 3, dan is de formule 4 + 3x2.
Omdat we eerst moeten kwadrateren (macht), daarna vermenigvuldigen en dan pas moeten optellen komt eerst alles op het bordje behalve de optelling. In de nieuwe tussenstap heb je alleen nog kwadrateren (macht) en vermenigvuldigen. Het bordje komt dus alleen op de macht en niet op de vermenigvuldiging.
Als we kijken naar voorbeeld 4 van kopje 3, dan is de formule (3x + 1)2.
Volgens de formule moet er eerst worden vermenigvuldigd, daarna opgeteld en dan pas gekwadrateerd. Je werkt dus eerst de kwadraat weg door het bordje op alles behalve de kwadraat te leggen. Het bordje komt dus tussen de haakjes. In de nieuwe tussenstap heb je alleen nog de optelling en de vermenigvuldiging over. Het bordje komt op alles behalve de optelling.
Conclusie:
Je werkt dus eigenlijk de voorrangsregels in de formule van achteren naar voren af om de vergelijking op te lossen. Dit is nog duidelijker bij de omgekeerde pijlenketting.